|
В физических и геометрических задачах нужно прежде решить,
какую из величин взять за независимую переменную
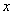 ,
а какую - за неизвестную функцию (или функции - при составлении систем ДУ) ,
а какую - за неизвестную функцию (или функции - при составлении систем ДУ)
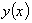 .
Затем нужно выразить, на сколько изменится значение искомой функции .
Затем нужно выразить, на сколько изменится значение искомой функции
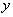 ,
когда независимая переменная ,
когда независимая переменная 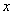 получит
приращение получит
приращение 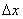 .
Затем выразить разность .
Затем выразить разность 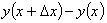 через
величины, о которых говорится в задаче. Разделив эту разность на через
величины, о которых говорится в задаче. Разделив эту разность на
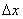 и
переходя к пределу при и
переходя к пределу при 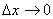 ,
получим дифференциальное уравнение. Иногда ДУ можно составить более простым
путем используя физический смысл производной. ,
получим дифференциальное уравнение. Иногда ДУ можно составить более простым
путем используя физический смысл производной.
№ 1. В сосуд, содержащий 10 л воды, непрерывно
поступает со скоростью 2 л в минуту раствор, в каждом литре которого содержится
0,3 кг соли. Поступающий в сосуд раствор перемешивается с водой, и смесь
вытекает из сосуда с той же скоростью. Сколько соли будет в сосуде через 5
минут?
Примем за независимую переменную время
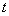 ,
а за неизвестную функцию ,
а за неизвестную функцию 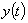 -
количество соли в сосуде через -
количество соли в сосуде через 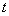 минут.
За промежуток времени от минут.
За промежуток времени от 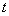 до до
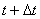 минут
количество соли в сосуде увеличивается из-за притока раствора на минут
количество соли в сосуде увеличивается из-за притока раствора на
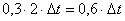 кг
соли. С другой стороны в вытекающих кг
соли. С другой стороны в вытекающих 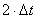 л
раствора содержится л
раствора содержится 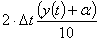 кг
соли, где кг
соли, где 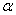 -
изменение количества соли за время -
изменение количества соли за время 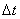 . .
Итак, во втекающем растворе содержится
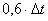 кг
соли, а в вытекающем - кг
соли, а в вытекающем - 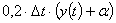 кг.
Приращение количества соли за это время кг.
Приращение количества соли за это время
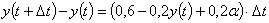 . .
Разделив эту разность на
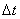 и
переходя к пределу при и
переходя к пределу при 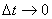 ,
получим дифференциальное уравнение ,
получим дифференциальное уравнение
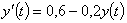 . .
Решая его, получим общее решение:
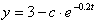 . .
Так как при 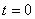 соли
в сосуде не было, то соли
в сосуде не было, то 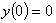 .
Найдем .
Найдем 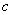 . .
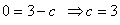 .
Частное решение: .
Частное решение: 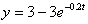 . .
Найдем количество соли в сосуде через 5 минут:
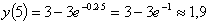 кг
соли. кг
соли.
№ 2. Составить систему дифференциальных уравнений
для задачи. «Тело массы 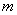 движется
на плоскости движется
на плоскости 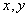 ,
притягиваясь к точке ,
притягиваясь к точке 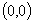 с
силой с
силой 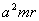 ,
где ,
где 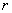 расстояние
до этой точки.» Найти движение тела при начальных условиях расстояние
до этой точки.» Найти движение тела при начальных условиях
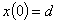 , ,
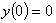 , ,
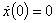 , ,
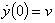 и
траекторию этого движения. и
траекторию этого движения.
Согласно второму закону Ньютона, система дифференциальных
уравнений движения имеет вид 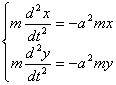 .
Эта система распадается на два уравнения. .
Эта система распадается на два уравнения.
Рассмотрим первое уравнение
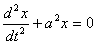  .
Это линейное однородное уравнение с постоянными коэффициентами с
характеристическим уравнением .
Это линейное однородное уравнение с постоянными коэффициентами с
характеристическим уравнением 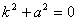 .
Решения характеристического уравнения .
Решения характеристического уравнения
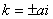 ,
соответствующее решение: ,
соответствующее решение: 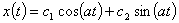 .
Аналогично для второго уравнения: .
Аналогично для второго уравнения: 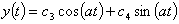 .
Найдем произвольные постоянные .
Найдем произвольные постоянные  . .
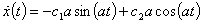 , ,
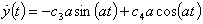 . .
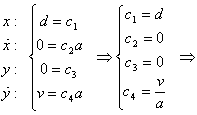 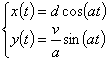 . .
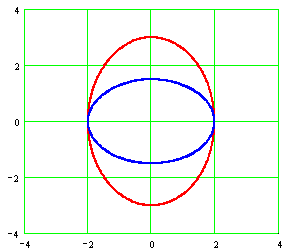
Последние уравнения являются параметрическим уравнением
эллипса с полуосями 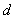 и и
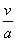 .
На рисунке показаны фазовые траектории для .
На рисунке показаны фазовые траектории для
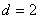 , ,
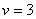 (красная (красная
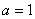 ,
синяя ,
синяя 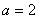 ). ).
В зависимости от величины
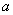 изменяется
периодичность движения. При изменяется
периодичность движения. При 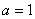 за
время за
время 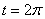 фазовая
точка пройдет один оборот (против часовой стрелки), а при фазовая
точка пройдет один оборот (против часовой стрелки), а при
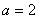 за
то же время - два оборота. за
то же время - два оборота.
Повторять ДУ и системы перед контрольной
№ 3. Один конец пружины закреплен неподвижно в точке
(0,0), а к другому при креплен груз массы
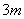 ,
соединенный другой пружиной с грузом массы ,
соединенный другой пружиной с грузом массы
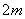 .
Оба груза двигаются без трения по одной прямой, проходящей через точку (0,0).
Каждая из пружин растягивается на величину .
Оба груза двигаются без трения по одной прямой, проходящей через точку (0,0).
Каждая из пружин растягивается на величину
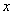 под
действием силы под
действием силы 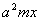 .
Найти возможные периодические движения системы. .
Найти возможные периодические движения системы.
№ 4. На концах вала закреплены два шкива, моменты
инерции которых 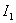 и и
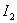 .
При повороте одного шкива относительно другого на любой угол .
При повороте одного шкива относительно другого на любой угол
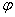 вследствие
деформации вала возникают упругие силы с крутящим моментом вследствие
деформации вала возникают упругие силы с крутящим моментом
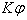 .
Найти частоту крутильных колебаний вала при отсутствии внешних сил. .
Найти частоту крутильных колебаний вала при отсутствии внешних сил.
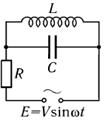
№ 5. К источнику тока с напряжением
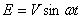 последовательно
присоединено сопротивление последовательно
присоединено сопротивление 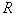 .
Далее цепь разветвляется на две ветви, в одной из которых включена самоиндукция .
Далее цепь разветвляется на две ветви, в одной из которых включена самоиндукция
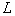 ,
а в другой - емкость ,
а в другой - емкость 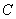 .
Найти силу тока в цепи (установившийся режим), проходящего через сопротивление .
Найти силу тока в цепи (установившийся режим), проходящего через сопротивление
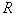 .
При какой частоте .
При какой частоте 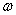 сила
тока наибольшая? Наименьшая? сила
тока наибольшая? Наименьшая?
№ 6. Какое условие достаточно наложить на
собственные значения матрицы A, чтобы система
уравнений (в векторной записи) 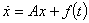 имела
периодическое решение при всякой непрерывной вектор - функции имела
периодическое решение при всякой непрерывной вектор - функции
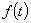 периода периода
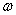 ? ?
Оформить и
сдать ИДЗ № 1 |