|

Вселенная играет в свои игры...
Кто вы? Игрушка в её руках? А может вы тот, в чьих руках может оказаться её судьба?
Мы расскажем вам про игры...
Игры Вселенной...
Узнать больше о книге.
Купить книгу (заказ через электронную почтовую форму)
С. Подклетнова. Игры Вселенной: НАЧАЛО. -
Москва, Россия: Издательство "Стигмарион", 2010 г., 400 с.
Стоимость книги 220 руб.
Бумажную версию книги можно приобрести на сайте издательства "Стигмарион"
Вопросы и предложения по распространению admin@big-biblioteka.com
|
|
|
|
|
| |
Вид частных решений для линейных неоднородных
дифференциальных уравнений с постоянными коэффициентами соответствует виду
правой части:
|
Вид правой части |
Вид числа
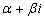 |
Кратность корня
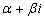 в
характеристическом уравнении, соответствующем однородному уравнению в
характеристическом уравнении, соответствующем однородному уравнению |
Вид частного решения |
|
Многочлен степени n:
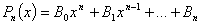
|
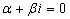
|
0 - не корень характеристического уравнения |
Многочлен степени n с
неопределенными коэффициентами
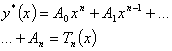
|
|
0 - корень характеристического уравнения кратности
p |
Многочлен степени n с
неопределенными коэффициентами, умноженный на
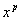
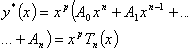
|
|
Произведение многочлена степени
n на 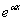 : :
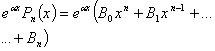 |
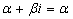
|
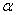 -
не корень характеристического уравнения -
не корень характеристического уравнения
|
Произведение многочлена степени
n с неопределенными коэффициентами на
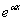 : :
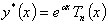 |
|
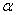 -
корень характеристического уравнения кратности p -
корень характеристического уравнения кратности p
|
Произведение многочлена степени
n с неопределенными коэффициентами на
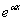 и и
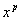 : :
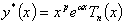 |
|
Выражение вида
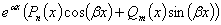
|
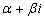 , ,
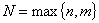
|
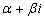 -
не корень характеристического уравнения -
не корень характеристического уравнения
|
Выражение вида
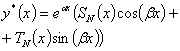 |
|
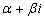 -
корень характеристического уравнения кратности p -
корень характеристического уравнения кратности p
|
Выражение вида
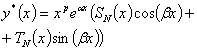 |
№ 1 Найдите общее решение дифференциального
уравнения 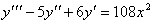 . .
Сначала найдем общее решение соответствующего линейного
однородного уравнения 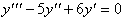 .
Составим для него характеристическое уравнение .
Составим для него характеристическое уравнение
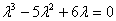 ,
корнями которого являются числа ,
корнями которого являются числа 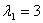 , ,
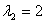 , ,
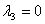 .
Тогда общее решение линейного однородного уравнения имеет вид .
Тогда общее решение линейного однородного уравнения имеет вид
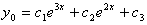 .
Правая часть ДУ - многочлен второй степени, число 0 является корнем
характеристического уравнения кратности 1. Согласно таблице, ищем частное
решение неоднородного уравнения в виде .
Правая часть ДУ - многочлен второй степени, число 0 является корнем
характеристического уравнения кратности 1. Согласно таблице, ищем частное
решение неоднородного уравнения в виде
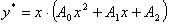 .
Для нахождения коэффициентов вычислим производные от .
Для нахождения коэффициентов вычислим производные от
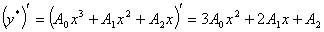 , ,
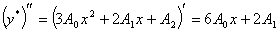 , ,
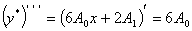 и
подставим их в уравнение. и
подставим их в уравнение.
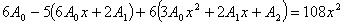 . .
Приравнивая коэффициенты при одинаковых степенях в левой и
правой частях последнего уравнения и составим систему:
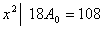 , ,
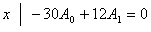 , ,
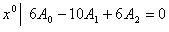 . .
Решим систему и найдем
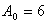 , ,
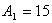 , ,
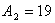 ,
тогда частное решение имеет вид ,
тогда частное решение имеет вид 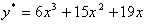 .
Общее решение имеет вид .
Общее решение имеет вид 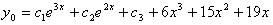 . .
№ 2 Найти общее решение дифференциального уравнения.
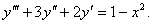
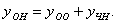
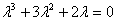 -характеристическое
уравнение. -характеристическое
уравнение.
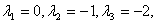
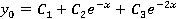 -
общее решение однородного уравнения. -
общее решение однородного уравнения.
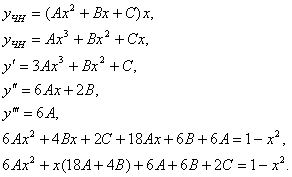
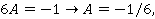
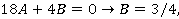
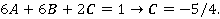
Отсюда

Общее решение
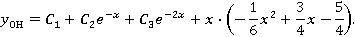
№ 3 Найти общее решение дифференциального уравнения.
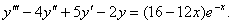
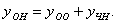
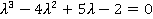 -
характеристическое уравнение. -
характеристическое уравнение.
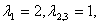
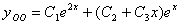 -общее решение
однородного уравнения. -общее решение
однородного уравнения.
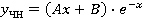 , ,
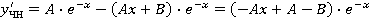 , ,
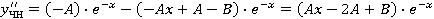 , ,
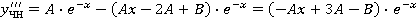 . .
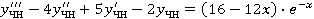 ; ;
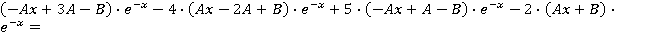
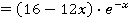 ; ;
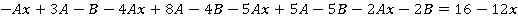 ; ;
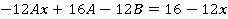 ; ;
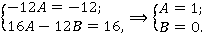
Отсюда
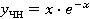 -
частное решение неоднородного уравнения. -
частное решение неоднородного уравнения.
Общее решение
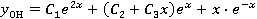 . .
№ 4 Найти общее решение дифференциального уравнения.
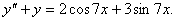
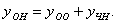
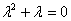 -характеристическое
уравнение. -характеристическое
уравнение.
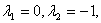
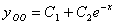 -общее решение
однородного уравнения. -общее решение
однородного уравнения.
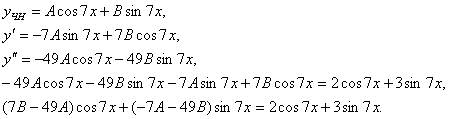
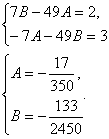
Отсюда 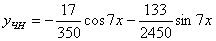 - частное решение
неоднородного уравнения. - частное решение
неоднородного уравнения.
Общее решение 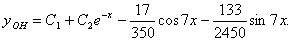
№ 5 Найти общее решение дифференциального уравнения.
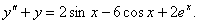
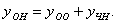
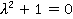 -характеристическое
уравнение. -характеристическое
уравнение.
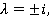
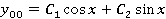 -
общее решение однородного уравнения. -
общее решение однородного уравнения.
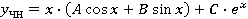 , ,
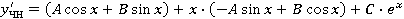 , ,
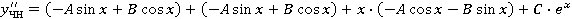 , ,
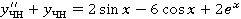 , ,
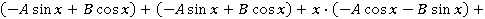
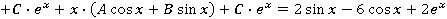 ; ;
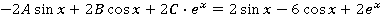 ; ;
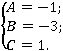
Отсюда
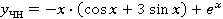 -
частное решение неоднородного уравнения. -
частное решение неоднородного уравнения.
Общее решение
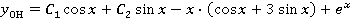 . .
Решить
задания 3 - 6 ИДЗ №1 с учетом правой части. | |
|