|
|
|
Функция распределения вероятностей случайной величины. Плотность распределения вероятности непрерывной случайной величины8.1. Функция распределения вероятностей случайной величины8.1.1. Определение функции распределенияВспомним, что дискретная случайная величина может быть задана перечнем всех ее возможных значений и их вероятностей. Такой способ задания не является общим: он неприменим, например, для непрерывных случайных величин. Действительно, рассмотрим случайную величину Пусть Функцией распределения называют функцию
Геометрически это равенство можно истолковать так: Иногда вместо термина «функция распределения» используют термин «интегральная функция». Теперь можно дать более точное определение непрерывной случайной величины: случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной. 8.1.2. Свойства функции распределенияСвойство 1.
Значения функции распределения принадлежат отрезку
Доказательство. Свойство вытекает из определения функции распределения как вероятности: вероятность всегда есть неотрицательное число, не превышающее единицы. Свойство 2.
Доказательство.
Пусть По теореме сложения имеем
Отсюда
или
Так как любая вероятность есть число неотрицательное, то Следствие 1.
Вероятность того, что случайная величина примет значение, заключенное в
интервале
Это важное следствие вытекает из формулы (8.1), если
положить Пример 8.1.
Случайная величина
Найти вероятность того, что в результате испытания Решение. Так как
на интервале
то
Итак,
Следствие 2.
Вероятность того, что непрерывная случайная величина Действительно, положив в формуле (8.2)
Устремим
Например, равенство
Таким образом, не представляет интереса говорить о вероятности того, что непрерывная случайная величина примет одно определенное значение, но имеет смысл рассматривать вероятность попадания ее в интервал, пусть даже сколь угодно малый. Этот факт полностью соответствует требованиям практических задач. Например, интересуются вероятностью того, что размеры деталей не выходят за дозволенные границы, но не ставят вопроса о вероятности их совпадения с проектным размером. Заметим, что было бы неправильным думать, что равенство
нулю вероятности Свойство 3.
Если возможные значения случайной величины принадлежат интервалу Доказательство. 1) Пусть 2) Пусть Следствие.
Если возможные значения непрерывной случайной величины расположены на всей оси
8.1.3. График функции распределенияДоказанные свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины. График расположен в полосе, ограниченной прямыми При возрастании При График функции распределения непрерывной случайной величины изображен на рис. 2.
Рис. 8.1
Замечание. График функции распределения дискретной случайной величины имеет ступенчатый вид. Убедимся в этом на примере. Пример 8.1.
Дискретная случайная величина
Найти функцию распределения и вычертить ее график. Решение. Если Если Если Если Итак, функция распределения аналитически может быть записана так:
График этой функции приведен на рис. 8.2.
Рис. 8.2. 8.2. Плотность распределения вероятностей
|
|
|
(8.4) |
Геометрически полученный результат можно истолковать так:
вероятность того, что непрерывная случайная величина примет значение,
принадлежащее интервалу ![]() ,
равна площади криволинейной трапеции, ограниченной осью
,
равна площади криволинейной трапеции, ограниченной осью ![]() ,
кривой распределения
,
кривой распределения ![]() и
прямыми
и
прямыми ![]() и
и
![]() .
.
Замечание. В
частности, если ![]() —
четная функция и концы интервала симметричны относительно начала координат, то
—
четная функция и концы интервала симметричны относительно начала координат, то
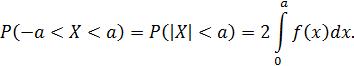
Пример 8.2.
Задана плотность вероятности случайной величины ![]()
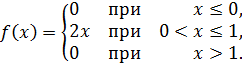
Найти вероятность того, что в результате испытания ![]() примет
значение, принадлежащее интервалу
примет
значение, принадлежащее интервалу ![]() .
.
Решение. Искомая вероятность
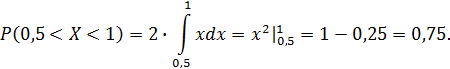
Зная плотность распределения ![]() ,
можно найти функцию распределения
,
можно найти функцию распределения ![]() по
формуле
по
формуле
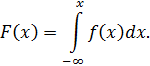
Действительно, мы обозначили через ![]() вероятность
того, что случайная величина примет значение, меньшее
вероятность
того, что случайная величина примет значение, меньшее ![]() ,
т.е.
,
т.е.
![]()
Очевидно, неравенство ![]() можно
записать в виде двойного неравенства
можно
записать в виде двойного неравенства ![]() ,
следовательно,
,
следовательно,
|
|
(8.5) |
Полагая в формуле (8.1) ![]() ,
,
![]() ,
имеем
,
имеем

Наконец, заменив ![]() на
на
![]() ,
в силу (8.5), окончательно получим
,
в силу (8.5), окончательно получим

Таким образом, зная плотность распределения, можно найти функцию распределения. Разумеется, по известной функции распределения может быть найдена плотность распределения, а именно:
![]()
Пример 8.3. Найти функцию распределения по данной плотности распределения:

Построить график найденной функции.
Решение. Воспользуемся формулой

Если ![]() ,
то
,
то ![]() ,
следовательно,
,
следовательно, ![]() .
Если
.
Если ![]() ,
то
,
то ![]() ,
следовательно,
,
следовательно,

Если ![]() то
то

Итак, искомая функция распределения

График этой функции изображен на рис. 8.3.

Рис. 8.3.
Свойство 1. Плотность распределения — неотрицательная функция:
![]()
Доказательство.
Функция распределения — неубывающая функция, следовательно, ее производная ![]() —
функция неотрицательная.
—
функция неотрицательная.
Геометрически это свойство означает, что точки,
принадлежащие графику плотности распределения, расположены либо над осью ![]() ,
либо на этой оси.
,
либо на этой оси.
График плотности распределения называют кривой распределения.
Свойство 2.
Несобственный интеграл от плотности распределения в пределах от -∞ до ![]() равен
единице:
равен
единице:

Доказательство. Несобственный интеграл

выражает вероятность события,
состоящего в том, что случайная величина примет значение, принадлежащее
интервалу ![]() .
Очевидно, такое событие достоверно, следовательно, вероятность его равна
единице.
.
Очевидно, такое событие достоверно, следовательно, вероятность его равна
единице.
Геометрически это означает, что вся площадь криволинейной
трапеции, ограниченной осью ![]() и
кривой распределения, равна единице.
и
кривой распределения, равна единице.
В частности, если все возможные значения случайной величины
принадлежат интервалу ![]() ,
то
,
то

Пример 8.4.
Плотность распределения случайной величины ![]() задана:
задана:
![]()
Найти постоянный параметр ![]() .
.
Решение.
Плотность распределения должна удовлетворять условию

поэтому потребуем, чтобы выполнялось равенство

Отсюда

Найдем неопределенный интеграл:
![]()
Вычислим несобственный интеграл:

![]()
Таким образом, искомый параметр
![]()
Пусть ![]() —
функция распределения непрерывной случайной величины
—
функция распределения непрерывной случайной величины ![]() .
По определению плотности распределения,
.
По определению плотности распределения, ![]() ,
или в иной форме
,
или в иной форме
![]()
Как уже известно, разность ![]() определяет
вероятность того, что
определяет
вероятность того, что ![]() примет
значение, принадлежащее интервалу
примет
значение, принадлежащее интервалу ![]() .
Таким образом, предел отношения вероятности того, что непрерывная случайная
величина примет значение, принадлежащее интервалу
.
Таким образом, предел отношения вероятности того, что непрерывная случайная
величина примет значение, принадлежащее интервалу ![]() .,
к длине этого интервала (при
.,
к длине этого интервала (при ![]() )
равен значению плотности распределения в точке
)
равен значению плотности распределения в точке ![]() .
.
По аналогии с определением плотности массы в точке[1]
целесообразно рассматривать значение функции ![]() в
точке
в
точке ![]() как
плотность вероятности в этой точке.
как
плотность вероятности в этой точке.
Итак, функция ![]() определяет
плотность распределения вероятности для каждой точки
определяет
плотность распределения вероятности для каждой точки ![]() .
.
Из дифференциального исчисления известно, что приращение функции приближенно равно дифференциалу функции, т.е.
![]()
или
![]()
Так как ![]() и
и
![]() ,
то
,
то
![]()
Вероятностный смысл этого равенства таков: вероятность
того, что случайная величина примет значение, принадлежащее интервалу ![]() ,
приближенно равна (с точностью до бесконечно малых высшего порядка относительно
,
приближенно равна (с точностью до бесконечно малых высшего порядка относительно ![]() )
произведению плотности вероятности в точке
)
произведению плотности вероятности в точке ![]() на
длину интервала
на
длину интервала ![]() .
.
Геометрически этот результат можно истолковать так:
вероятность того, что случайная величина примет значение, принадлежащее
интервалу ![]() ,
приближенно равна площади прямоугольника с основанием
,
приближенно равна площади прямоугольника с основанием ![]() и
высотой
и
высотой ![]() .
.
На рис. 8.4 видно, что площадь заштрихованного
прямоугольника, равная произведению ![]() ,
лишь приближенно равна площади криволинейной трапеции (истинной вероятности,
определяемой определенным интегралом
,
лишь приближенно равна площади криволинейной трапеции (истинной вероятности,
определяемой определенным интегралом ![]() ).
Допущенная при этом погрешность равна площади криволинейного треугольника
).
Допущенная при этом погрешность равна площади криволинейного треугольника ![]() .
.

Рис. 8.4.
При решении задач, которые выдвигает практика, приходится сталкиваться с различными распределениями непрерывных случайных величин. Плотности распределений непрерывных случайных величин называют также законами распределений. Часто встречаются, например, законы равномерного, нормального и показательного распределений. В настоящем параграфе рассматривается закон равномерного распределения вероятностей.
Нормальному и показательному законам посвящены следующие две главы.
Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
Приведем пример равномерно распределенной непрерывной случайной величины.
Пример 8.5.
Шкала измерительного прибора проградуирована в некоторых единицах. Ошибку при
округлении отсчета до ближайшего целого деления можно рассматривать как
случайную величину ![]() ,
которая может принимать с постоянной плотностью вероятности любое значение между
двумя соседними целыми делениями. Таким образом,
,
которая может принимать с постоянной плотностью вероятности любое значение между
двумя соседними целыми делениями. Таким образом, ![]() имеет
равномерное распределение.
имеет
равномерное распределение.
Найдем плотность равномерного распределения ![]() ,
считая, что все возможные значения случайной величины заключены в интервале
,
считая, что все возможные значения случайной величины заключены в интервале ![]() ,
на котором функция
,
на котором функция ![]() сохраняет
постоянные значения:
сохраняет
постоянные значения:
По условию, ![]() не
принимает значений вне интервала
не
принимает значений вне интервала ![]() ,
поэтому
,
поэтому ![]() при
при
![]() и
и
![]() .
.
Найдем постоянную ![]() .
Так как все возможные значения случайной величины принадлежат интервалу
.
Так как все возможные значения случайной величины принадлежат интервалу ![]() ,
то должно выполняться соотношение
,
то должно выполняться соотношение

или

Отсюда

Итак, искомая плотность вероятности равномерного распределения

График плотности равномерного распределения изображен на рис. 8.5, а график функции распределения — на рис. 8.3.

Рис. 8.5.
Замечание.
Обозначим через ![]() непрерывную
случайную величину, распределенную равномерно в интервале
непрерывную
случайную величину, распределенную равномерно в интервале ![]() ,
а через
,
а через ![]() —
ее возможные значения. Вероятность попадания величины
—
ее возможные значения. Вероятность попадания величины ![]() (в
результате испытания) в интервал
(в
результате испытания) в интервал ![]() ,
принадлежащий интервалу
,
принадлежащий интервалу ![]() ,
равна его длине:
,
равна его длине:
![]()
Действительно, плотность рассматриваемого равномерного распределения
![]()
Следовательно, вероятность попадания случайной величины ![]() в
интервал
в
интервал ![]()

[1] Если масса непрерывно распределена вдоль оси ![]() по
некоторому закону, например
по
некоторому закону, например ![]() ,
то плотностью
,
то плотностью ![]() массы
в точке
массы
в точке ![]() называют
предел отношения массы интервала
называют
предел отношения массы интервала ![]() к
длине интервала при
к
длине интервала при ![]() ,
т.е.
,
т.е.
![]()
|